Слайды и текст этой онлайн презентации
Слайд 1
Раздел 3 . Прямые и плоскости в пространстве 3.1 Прямые в пространстве 3.1.1 Взаимное расположение двух прямых в пространстве. 3.1.2 Параллельность прямой и плоскости.
Слайд 2
Стереометрия – раздел геометрии, в котором изучаются фигуры в пространстве. Основные понятия стереометрии: точка, прямая, плоскость и расстояние от точки до точки. В стереометрии изучают свойства фигур, не все точки которых лежат в одной плоскости – пространственных фигур . Геометрическое тело – часть пространства, занимаемая предметом и изучаемая относительно её формы и размера, независимо от физических свойств предмета. Геометрическое тело отделяется от окружающего пространства поверхностью .
Слайд 3
Равными (конгруэнтными) фигурами называются такие две фигуры, которые можно совместить так, чтобы они совпали во всех своих частях. Две фигуры, состоящие из одних и тех же точек, мы будем рассматривать как одну и ту же фигуру.
Слайд 4
Основной геометрической образ стереометрии – плоскость. Свойства плоскости, принимаемые без доказательств: Плоскость есть поверхность незамкнутая (безграничная), но на чертеже условно обозначается в виде параллелограмма и обозначается буквой греческого алфавита (например, плоскость
Слайд 5
Любая плоскость делит пространство на две области, расположенные по разные стороны от этой плоскости Если прямая имеет с плоскостью только одну общую точку, то она ее пересекает, переходя из части пространства, лежащей по одну сторону плоскости, в часть пространства, лежащую по другую её сторону.
Слайд 6
Аксиомы стериометрии: Аксиома 1: Через любые три точки пространства, не лежащие на одной прямой, можно провести плоскость, при том только одну.
Слайд 7
Аксиома 2: Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит: Фигура, являющаяся прямой в одной плоскости, является прямой и в любой другой плоскости, на которой она лежит. Поэтому, прямую в пространстве можно рассматривать саму по себе, независимо от плоскостей, в которых она лежит.
Слайд 8
Аксиома 3: Если две точки прямой лежат на плоскости, то и вся прямая лежит на той же плоскости. Значит: Если прямая не лежит на плоскости, то она имеет с ней не более одной общей точки.
Слайд 9
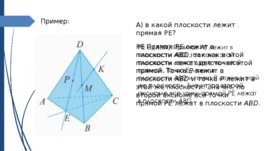
Пример: А) в какой плоскости лежит прямая РЕ? РЕ Прямая РЕ лежит в плоскости АВD , так как в этой плоскости лежат две точки этой прямой. Точка Е лежит в плоскости АВD и точка Р лежит в этой же плоскости. Значит, по второй аксиоме все точки прямой РЕ лежат в плоскости АВD .
Слайд 10
Аксиома 4: Расстояние между любыми двумя точками пространства одно и то же в любой плоскости, проходящей через эти точки. Следствие 1: Через прямую а и точку С вне ее можно провести плоскость, и при том только одну. Значит: На прямой а можно взять любые две точки, которые вместе с точкой С образуют три точки, не лежащие не на одной прямой по А1 через эти три точки можно провести плоскость, и при том только одну.
Слайд 11
Замечание: Через любую прямую в пространстве можно провести бесконечное множество плоскостей.
Слайд 12
Следствие 2: Через две пересекающиеся прямые можно провести плоскость, и притом только одну.
Слайд 13
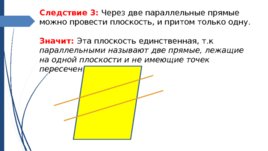
Следствие 3: Через две параллельные прямые можно провести плоскость, и притом только одну. Значит: Эта плоскость единственная, т.к параллельными называют две прямые, лежащие на одной плоскости и не имеющие точек пересечения.
Слайд 14
Аксиома (из планиметрии): Через точку, не лежащую на заданной прямой, нельзя провести более одной прямой, параллельной этой заданной прямой. Она справедлива и в стереометрии, тк если прямые в пространстве параллельны, то они лежат на одной плоскости.
Слайд 15
В пространстве две прямые могут: Лежать на одной плоскости, при этом : - иметь общую точку (пересекающиеся прямые) - не иметь общих точек (параллельные прямые) Не лежать на одной плоскости и не иметь общих точек
Слайд 16
Две прямые в пространстве, которые не имеют общих точек и не параллельны, называются скрещивающимися. Углом, между двумя скрещивающимися прямыми называется угол, который образуется двумя параллельными им лучами, исходящими из одной точки.
Слайд 17
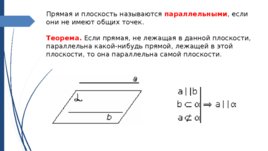
Прямая и плоскость называются параллельными , если они не имеют общих точек. Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Слайд 18
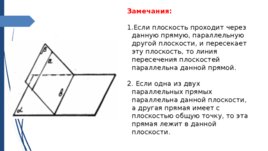
Замечания: Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. Если одна из двух параллельных прямых параллельна данной плоскости, а другая прямая имеет с плоскостью общую точку, то эта прямая лежит в данной плоскости.
Слайд 19
а) прямая лежит в плоскости;
б) прямая и плоскость имеют только одну общую точку;
в) прямая и плоскость не имеют ни одной общей точки. Случаи взаимного расположения прямой и плоскости:
Слайд 20
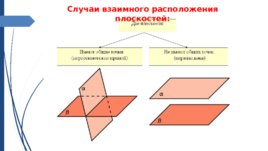
Случаи взаимного расположения плоскостей:
Слайд 21
Свойства параллельных плоскостей: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
 Прямые и плоскости в пространстве
Прямые и плоскости в пространстве Перпендикулярные прямые в пространстве
Перпендикулярные прямые в пространстве Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс
Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс Угол между лучами. Угол между прямыми в пространстве. Перпендикулярные прямые
Угол между лучами. Угол между прямыми в пространстве. Перпендикулярные прямые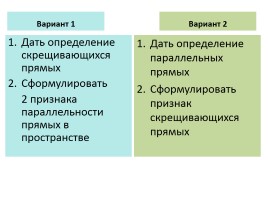 Блиц-опрос «Взаимное расположение прямых в пространстве»
Блиц-опрос «Взаимное расположение прямых в пространстве» Перпендикулярность прямых в пространстве
Перпендикулярность прямых в пространстве Взаимное расположение двух прямых в пространстве
Взаимное расположение двух прямых в пространстве