Презентация - Решение систем рациональных уравнений

Решение систем рациональных уравнений
ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ

Способы решения систем уравнений
Графический Способ подстановки Способ сложения Способ введения переменной

Способ подстановки
Из какого-либо уравнения выразить одну переменную через другую. Подставить полученное выражение для переменной в другое уравнение и решить его. Вычислить значение второй переменной. Записать ответ: (х ; у) .

Задача №1
х2-12х2-40х-9х2 -60х-100+20=0
-20х2-100х-80=0
Если х1=-4, то у1=-2. Если х2=-1, то у2=7.
х2+5х+4=0
х1=-4, х2=-1
Ответ:(-4;-2), (-1;7)

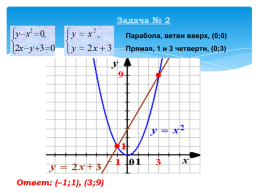
Задача № 2
Парабола, ветви вверх, (0;0) Прямая, 1 и 3 четверти, (0;3)
Ответ: (–1;1), (3;9)

Задача № 3
При каких значения b,c,k и l графики функций y=kx+l и y=x^2+bx+c пересекаются в точках А(6;4) и В(4;10)?

№4 Сумма длин катетов прямоугольного треугольника равна 23 см, а длина его гипотенузы равна 17 см. Найдите длину каждого катета.
x+y =23 x-y=17
x+y=23 x2+y2=172
a)
В)
x-y=23 X2+y2=17
x- y =17 x2-y2=17
Г)
б)

Способ сложения
Умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами. Сложить почленно левые и правые части уравнений системы. Решить получившееся уравнение с одной переменной. Подставить значение найденной переменной в одно из уравнений системы и найти значение другой переменной. Записать ответ: (х; у) .

Какой аналитический метод решения удобнее использовать?
.подстановки
.сложения
.сложения
.Введение новых переменных

Введение двух новых переменных для обоих уравнений системы
№1. Решить систему: Пусть тогда
1. Ввести две новые переменные для двух уравнений системы, тогда оба уравнения системы можно будет переписать в более простом виде. 2. Решить новую полученную систему с новыми неизвестными удобным способом (сложения или подстановки).

3. Подставить каждый корень, найденный на втором шаге, в две веденных постановки. 4. Записать поочередно полученные уравнения в систему. 5. Решить полученную систему уравнений удобным способом(методом сложения или подстановки). 6. Записать все пары полученных значений системы в ответ.
Вернемся к подстановке: Ответ (1;0).