Презентация - Решение задач с помощью кругов Эйлера

РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА.
Цель нашего урока
Рассмотреть способы решения задач с помощью кругов Эйлера
ВЫ УЗНАЕТЕ как проводить логические рассуждения по сюжетам текстовых задач с помощью кругов Эйлера

Устный счет

Контроль усвоения материала
Вариант 1. Задание № 1. Даны множества А = {2; 5; 7; 8; 12; 17} и В = {2; 3; 7; 9; 15; 17}. Найдите объединение и пересечение множеств. Задание № 2. Пусть A – множество трехзначных чисел, кратных 7, а B – множество трехзначных чисел, кратных 4. Сколько элементов содержит множество C = A ⋂ B? Задание № 3. Заданы множества: B – множество всех прямоугольников, C – множество всех ромбов, D – множество всех квадратов. Какое из указанных соотношений неверно? B ⋂ C = D, B ⋃ D = B, B ⋃ C = D, C ⋃ D = C
Вариант 2. Задание № 1. Даны множества А = {3; 5; 6; 8; 15; 19} и В = {2; 3; 7; 8; 16; 19}. Найдите объединение и пересечение множеств. Задание № 2. Пусть A – множество трехзначных чисел, кратных 6, а B – множество трехзначных чисел, кратных 3. Сколько элементов содержит множество C = A ⋂ B? Задание № 3. Заданы множества: B – множество всех прямоугольников, C – множество всех ромбов, D – множество всех квадратов. Какое из указанных соотношений неверно? B ⋃ D = D, B ⋂ C = D, B ⋃ C = D, C ⋃ D = C

Введение
В классе из 30 человек умеют плавать 20 учеников, 17 учеников умеют играть в шахматы, и только пятеро не умеют ни того ни другого. Сколько ребят умеют и плавать, и играть в шахматы?
Плавают или играют в шахматы 30 – 5 = 25 учеников С другой стороны таких учеников 20 + 17 = 37 Разные значения получились из-за того, что во второй раз мы дважды посчитали ребят, которые умеют и плавать, и играть в шахматы Значит, таких учеников 37 – 25 = 12

Введение
Число элементов множества, являющегося объединением двух множеств, можно вычислить как разность суммы чисел элементов двух данных множеств и числа элементов, принадлежащих одновременно двум множествам, то есть числа элементов множества, являющегося их пересечением.
На математическом языке это правило можно записать следующим образом: Пусть даны множества А и В, множество С = А ∩ В Тогда N(С) = N(А) + N(В) – N(А ∩ В) Формула включений и исключений.

Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?

Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Круги Эйлера отражают отношение между заданными множествами. Запишем число элементов каждого из полученных множеств. С = {сыр} В = {ветчина} К = {Колбаса} П = {пирожки} Начнем заполнять схему с центрального множества. Пересечением всех трех множеств – те, кто взял с собой все три вида бутербродов. Это по условию 19 человек.
С
В
П
К

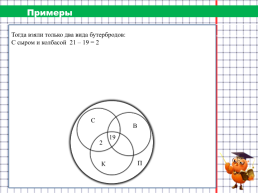
Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Тогда взяли только два вида бутербродов: С сыром и колбасой 21 – 19 = 2
С
В
П
К

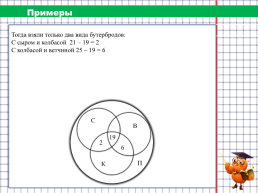
Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Тогда взяли только два вида бутербродов: С сыром и колбасой 21 – 19 = 2 С колбасой и ветчиной 25 – 19 = 6
С
В
П
К

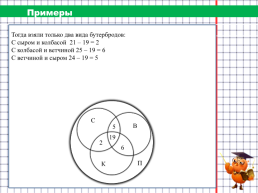
Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Тогда взяли только два вида бутербродов: С сыром и колбасой 21 – 19 = 2 С колбасой и ветчиной 25 – 19 = 6 С ветчиной и сыром 24 – 19 = 5
С
В
П
К

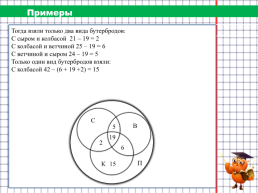
Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Тогда взяли только два вида бутербродов: С сыром и колбасой 21 – 19 = 2 С колбасой и ветчиной 25 – 19 = 6 С ветчиной и сыром 24 – 19 = 5 Только один вид бутербродов взяли: С колбасой 42 – (6 + 19 +2) = 15
С
В
П
К

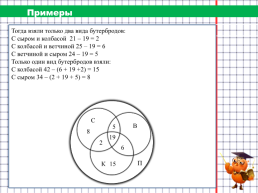
Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Тогда взяли только два вида бутербродов: С сыром и колбасой 21 – 19 = 2 С колбасой и ветчиной 25 – 19 = 6 С ветчиной и сыром 24 – 19 = 5 Только один вид бутербродов взяли: С колбасой 42 – (6 + 19 +2) = 15 С сыром 34 – (2 + 19 + 5) = 8
С
В
П
К

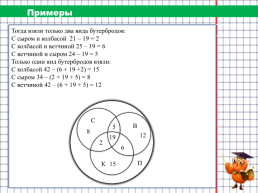
Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Тогда взяли только два вида бутербродов: С сыром и колбасой 21 – 19 = 2 С колбасой и ветчиной 25 – 19 = 6 С ветчиной и сыром 24 – 19 = 5 Только один вид бутербродов взяли: С колбасой 42 – (6 + 19 +2) = 15 С сыром 34 – (2 + 19 + 5) = 8 С ветчиной 42 – (6 + 19 + 5) = 12
С
В
П
К

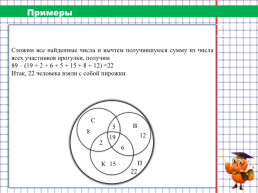
Примеры
На загородную прогулку поехали 89 человек. Бутерброды с колбасой взяли 42 человека, с сыром – 34 человека, с ветчиной – 42 человека, с сыром и колбасой – 21 человек, с колбасой и ветчиной – 25 человек, а с сыром и с ветчиной – 24 человека. 19 человек взяли с собой все три вида бутербродов, а несколько человек вместо бутербродов взяли пирожки. Сколько человек взяли с собой пирожки?
Сложим все найденные числа и вычтем получившуюся сумму из числа всех участников прогулки, получим 89 – (19 + 2 + 6 + 5 + 15 + 8 + 12) =22 Итак, 22 человека взяли с собой пирожки.
С
В
П
К

Рефлексия
Леонард Эйлер (1707 Базель, Швейцария – 1783 Санкт-Петербург, Российская империя) швейцарский, немецкий и российский математик и механик. Входит в пятерку величайших математиков в истории.

Задание на дом
Домашнее задание тема 10.3 (стр. 218 – 219) изучить; письменно выполнить № 833 № 834 № 837
УЧЕБНИК
ТЕТРАДЬ