Презентация - Применение признаков делимости в 6 классе

Применение признаков делимости в 6 классе

Знание и использование признаков делимости натуральных чисел способствуют эффективному и рациональному решению задач.

Биография Эратосфена
Эратосфен Киренский (276-194 гг. до н.э.) - древнегреческий ученый, математик, астроном. Самым знаменитым математическим открытием стало так называемое «решето»

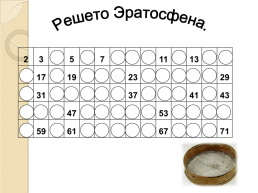
Решето Эратосфена.
2.3.4.5.6.7.8.9.10.11.12.13.14.15
16.17.18.19.20.21.22.23.24.25.26.27.28.29
30.31.32.33.34.35.36.37.38.39.40.41.42.43
44.45.46.47.48.49.50.51.52.53.54.55.56.57
58.59.60.61.62.63.64.65.66.67.68.69.70.71

Пифагор Самосский
Понятие простого числа было введено Пифагором еще в IV веке до н.э.. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, 6=1+2+3; 28=1+2+7+4+14 и т.д.

Простые числа
В III веке до н.э. Евклид доказал, что простых чисел бесконечно много, то есть за каждым простым числом есть еще большее простое число.

Блез Паскаль
Нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число

Классификация признаков делимости:
1. Делимость по последним цифрам числа; 2. Делимость по сумме цифр числа; 3. Делимость составных чисел.

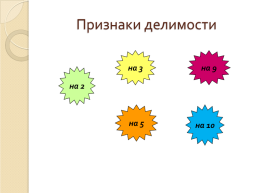
Признаки делимости
на 3
на 9
на 2
на 5
на 10

Признаки делимости чисел
Признаки делимости на 4. Число делится на 4 из двух последних его цифр делится на 4. 135 456 делится на 4, т.к. 56 : 4 = 14 Признак делимости на 8. Число делится на 8 три его последние цифры – нули или образуют число, которое делится на 8. 21 952 делится на 8, т.к. 952 : 8 = 119

Признаки делимости на 25. Число делится на 25 число образованное его последними двумя цифрами делится на 25. 652 475 делится на 25, т.к. 75 делится на 25 Признаки делимости на 125. Число делится на 125 число образованное его последними тремя цифрами делится на 125 354 250 делится на 125, т.к. 250 : 125 = 2

Признак Паскаля:
Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число. 2814 делится на 7, т.к. 2·6 + 8 ·2 + 1 ·3 +4 = 35, 35:7=5 (где 6 – остаток от деления 1000 на 7; 2 - остаток от деления 100 на 7, 3 - остаток от деления 10 на 7)

Другие признаки делимости, следующие из двух признаков
Признак делимости на 6. Число делится на 6 оно делится и на 2, и на 3. (456) Признак делимости на 12. Число делится на 12 оно делится и на 3, и на 4. (589 524) Признак делимости на 14. Число делится на 14 оно делится и на 2, и на 7. (364) Признак делимости на 15. Число делится на 15 оно делится и на 3, и на 5. (8 445)

«Предмет математики настолько серьёзен, что нужно не упускать случая, делать его немного занимательным.» Блез Паскаль

Применение признаков делимости натуральных чисел при решении задач ЕГЭ.
Задача Найти такие четырёхзначные числа, каждое из которых делится на 11, а сумма цифр каждого числа равна 11.

Решение
Общий вид четырёхзначного числа: 1000х+100у+10z+u. По условию задачи имеем: х + y +z + u=11. (1) По признаку делимости чисел на 11 имеем: ((x+z)-(y+u)):11=k, (2) где k – целое число. 0 ≤ х ≤ 9, 0 ≤ y ≤ 9, 0 ≤ z ≤ 9, 0 ≤u ≤ 9. 0 ≤ х + z ≤ 18, 0 ≤ y+u ≤ 18. Тогда0 ≥ -( y+u) ≥ -18, т.е., -18 ≤ -( y+u) ≤ 0. Складывая два верных числовых неравенства: 0 ≤ х + z ≤ 18 (3) -18 ≤ -( y+u) ≤ 0. (4) Получаем: - 18 ≤ (х+z)- (y+u) ≤ 18 -18 ≤ 11∙k ≤ 18, то есть, - 18/11≤ k ≤ 18/11. Значит, k может быть -1; 0; 1.

Исследуем возможные значения k. Из выражения (2) имеем: (х+z)- (y+u) = 11∙k. (5) k = 0. Складывая выражения (1) и (5) получаем 2∙ (х + z) = 11∙ (1+k) (6) Замечаем, что в левой части равенства число четное. Следовательно, и в правой части должно быть четное число; отсюда следует, что k≠0. k = -1. В этом случае, из выражения (6) получим, что х+z=0. Однако при x=0 искомое число будет трёхзначным; следовательно, k≠-1. Остается принять, что k = 1. k = 1. Вычитая из равенства (1) равенство (5) получаем 2 ∙ (y+u) = 11 (1-k). Так как k = 1, то y+u=0. Это возможно, если y=0, u=0. Из равенства (6) при k = 1 имеем, что х + z=11. Но если х будет меняться от 2 до 9, то z будет изменяться от 9до 2. Вследствие этого получаем искомые четырехзначные числа: 2090, 3080, 4070, 5060, 6050, 7040, 8030, 9020. Ответ: 2090, 3080, 4070, 6050, 7040, 8030, 9020.

Задача
Вычеркните в числе 53164018 три цифры так, чтобы получившееся число делилось на 15. В ответе укажите ровно одно получившееся число. Решение: Чтобы число делилось на 15, надо, чтобы оно делилось на 3 и на 5. Чтобы число делилось на 5, надо, чтобы оно оканчивалось на 0 или на 5. Вычеркнем 2 последние цифры, получится 531640. Из этого числа надо вычеркнуть одну цифру, так, чтобы оставшееся число делилось на 3. По признаку делимости на 3 проверяем сумму цифр числа: 5+3++1+6+4+0=19. Если в записи последнего числа вычеркнем число 1, то получится число 53640 (сумма цифр числа 18), значит, число будет делиться без остатка на 3. Если вычеркнем цифру 4, то получится число 53160 (сумма цифр равна 15). Таким образом, мы получили два числа: 53640 и 53160. В ответе запишем одно из этих чисел, например, число 53640. Ответ: 53640

Заключение
Полученные знания можно использовать в учебной деятельности, самостоятельно применить тот или иной признак к определенной задаче, применить изученные признаки в реальной ситуации. Рекомендуется использовать материал учащимся 11 классов при подготовке к ЕГЭ.