Презентация - Скрещивающиеся прямые (решение задач 1 часть)
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 87%
- Слайдов: 35
- Просмотров: 5019
- Скачиваний: 1831
- Размер: 0.83 MB
- Класс: 10
- Формат: ppt / pptx
Примеры похожих презентаций
 Скрещивающиеся прямые (решение задач)
Скрещивающиеся прямые (решение задач) Решение задач по теме «Параллельные прямые»
Решение задач по теме «Параллельные прямые» Решение задач ОГЭ «Модуль геометрия» Часть 2
Решение задач ОГЭ «Модуль геометрия» Часть 2 Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс
Решение задач по теме: «аксиомы стереометрии. Взаимное расположение прямых в пространстве. Угол между двумя прямыми". Геометрия 10 класс Решение задач «Параллельные прямые»
Решение задач «Параллельные прямые» Использование таблиц для решения задач
Использование таблиц для решения задач Урок в 5 классе «Решение практических задач»
Урок в 5 классе «Решение практических задач»
Слайды и текст этой онлайн презентации
Слайд 1

Скрещивающиеся Л. С. Атанасян Геометрия 10 класс прямые
Слайд 2

Взаимное расположение двух прямых в пространстве: a b a b a b ?
Слайд 3
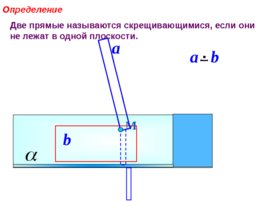
Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Определение М a b a b
Слайд 4
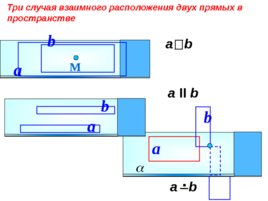
а II b Три случая взаимного расположения двух прямых в пространстве а b М a b a b a b а b
Слайд 5
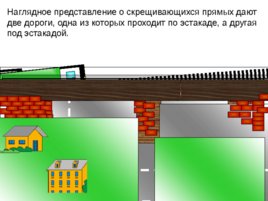
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой.
Слайд 6
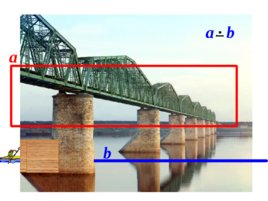
a b a b
Слайд 7
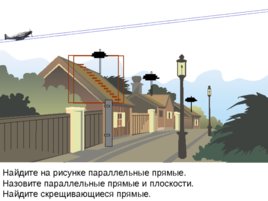
Найдите на рисунке параллельные прямые. Назовите параллельные прямые и плоскости. Найдите скрещивающиеся прямые.
Слайд 8
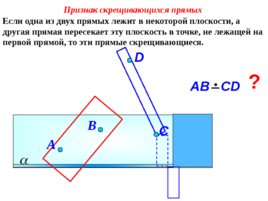
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся. Признак скрещивающихся прямых D В АВ С D А C ?
Слайд 9
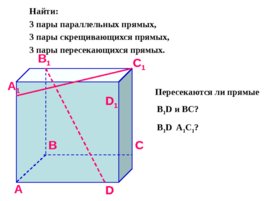
A B C D A 1 B 1 C 1 D 1 Найти: 3 пары параллельных прямых, 3 пары скрещивающихся прямых, 3 пары пересекающихся прямых. Пересекаются ли прямые B 1 D и BC ? B 1 D A 1 C 1 ?
Слайд 10
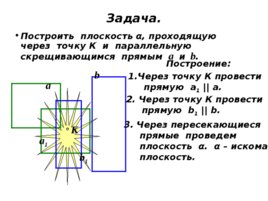
Задача. Построить плоскость α , проходящую через точку К и параллельную скрещивающимся прямым а и b . Построение: Через точку К провести прямую а 1 а. 2. Через точку К провести прямую b 1 b . а b К а 1 b 1 3 . Через пересекающиеся прямые проведем плоскость α . α – искомая плоскость.
Слайд 11
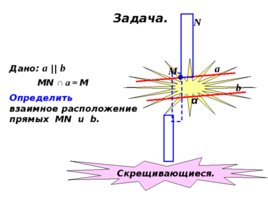
Задача. α a b М N Дано: a b MN a M Определить взаимное расположение прямых MN u b . Скрещивающиеся.
Слайд 12
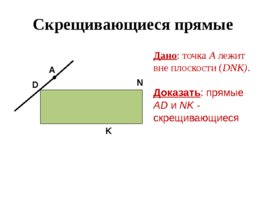
Скрещивающиеся прямые Дано : точка А лежит вне плоскости ( DNK ) . Доказать : прямые AD и NK - скрещивающиеся А K N D
Слайд 13
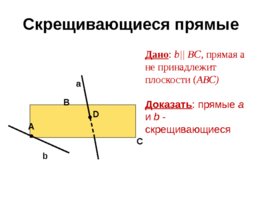
Скрещивающиеся прямые Дано : b BC , прямая а не принадлежит плоскости ( АВС) Доказать : прямые a и b - скрещивающиеся b а А С В D
Слайд 14
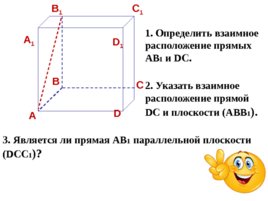
В А А 1 В 1 С 1 D 1 С D 1. Определить взаимное расположение прямых АВ 1 и DC . 2 . Указать взаимное расположение прямой DC и плоскости (АВВ 1 ). 3. Является ли прямая АВ 1 параллельной плоскости ( D СС 1 )?
Слайд 15
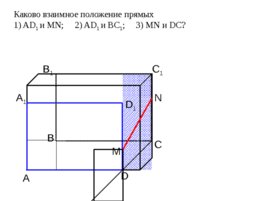
А D С В B 1 С 1 D 1 А 1 Каково взаимное положение прямых 1) AD 1 и М N; 2) AD 1 и ВС 1 ; 3) М N и DC ? N M
Слайд 16
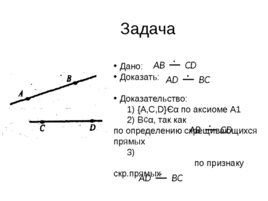
Задача Дано: Доказать: Доказательство: 1) A,C,D Є α по аксиоме А1 2) В α , так как по определению скрещивающихся прямых 3) по признаку скр.прямых AB CD AD BC AB CD AD BC
Слайд 17
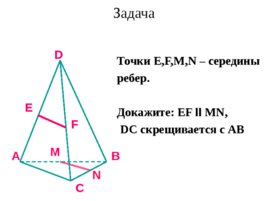
Задача A B C D E F M N Точки Е, F,M,N – середины ребер. Докажите: EF ll MN, DC скрещивается с AB
Слайд 18
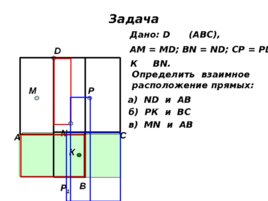
Задача А В С D M N P Р 1 К Дано: D (АВС), АМ М D ; В N ND; CP PD К В N . Определить взаимное расположение прямых: а) ND и AB б) РК и ВС в) М N и AB
Слайд 19
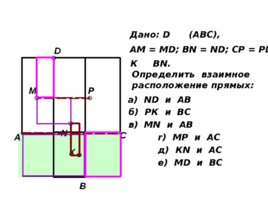
А В С D M N P К Дано: D (АВС), АМ М D ; В N ND; CP PD К В N . Определить взаимное расположение прямых: а) ND и AB б) РК и ВС в) М N и AB г) МР и A С д) К N и A С е) М D и B С
Слайд 20
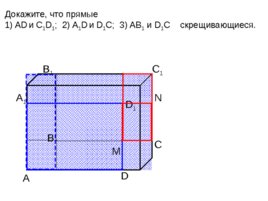
А D С В B 1 С 1 D 1 А 1 Докажите, что прямые 1) AD и C 1 D 1 ; 2) A 1 D и D 1 C ; 3) AB 1 и D 1 C скрещивающиеся. N M
Слайд 21
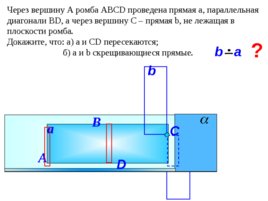
Через вершину А ромба АВС D проведена прямая а, параллельная диагонали В D , а через вершину С – прямая b , не лежащая в плоскости ромба. Докажите, что: а) а и С D пересекаются; б) а и b скрещивающиеся прямые. В b a А C ? a b D
Слайд 22
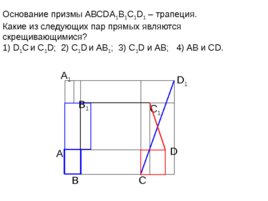
А D С В B 1 С 1 D 1 А 1 Основание призмы АВС DA 1 B 1 C 1 D 1 – трапеция. Какие из следующих пар прямых являются скрещивающимися? 1) D 1 C и C 1 D; 2) C 1 D и AB 1 ; 3) C 1 D и AB; 4) AB и CD.
Слайд 23
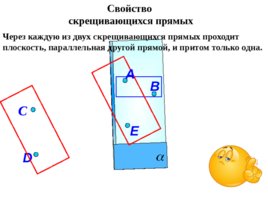
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. D С B E A Свойство скрещивающихся прямых
Слайд 24
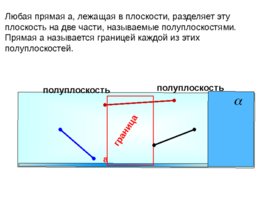
полуплоскость полуплоскость граница Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. а
Слайд 25
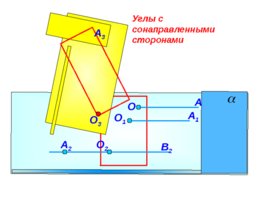
Углы с сонаправленными сторонами A О О 1 О 2 A 1 В 2 A 2 О 3 A 3
Слайд 26
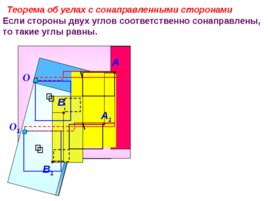
Если стороны двух углов соответственно сонаправлены, то такие углы равны. Теорема об углах с сонаправленными сторонами О О 1 A 1 A B 1 B
Слайд 27
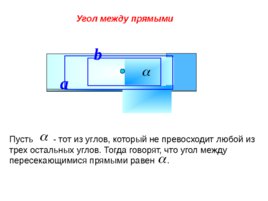
Угол между прямыми a b Пусть - тот из углов, который не превосходит любой из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен .
Слайд 28
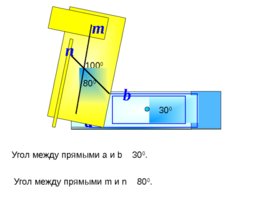
a b 30 0 n 10 0 0 m 8 0 0 Угол между прямыми m и n 80 0 . Угол между прямыми а и b 30 0 .
Слайд 29
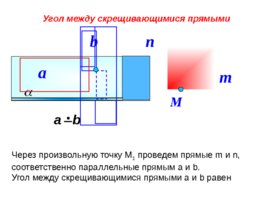
Угол между скрещивающимися прямыми а b a b b М Через произвольную точку М 1 проведем прямые m и n , соответственно параллельные прямым a и b . Угол между скрещивающимися прямыми a и b равен m n
Слайд 30
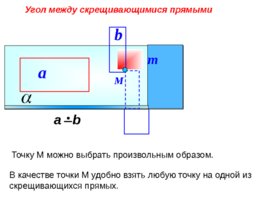
Угол между скрещивающимися прямыми а b a b М Точку М можно выбрать произвольным образом. m В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых.
Слайд 31
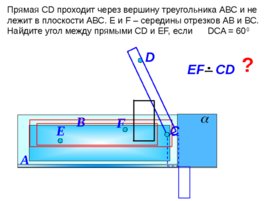
Прямая С D проходит через вершину треугольника АВС и не лежит в плоскости АВС. E и F – середины отрезков АВ и ВС. Найдите угол между прямыми С D и EF , если DCA 60 0 D В EF С D А C ? F E
Слайд 32
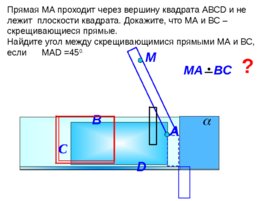
Прямая МА проходит через вершину квадрата АВС D и не лежит плоскости квадрата. Докажите, что МА и ВС – скрещивающиеся прямые. Найдите угол между скрещивающимися прямыми МА и ВС, если МА D 45 0. М D МА ВС С А ? B
Слайд 33
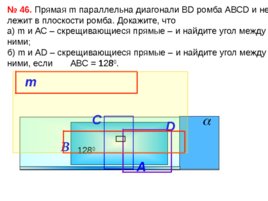
т № 46. Прямая m параллельна диагонали В D ромба АВС D и не лежит в плоскости ромба. Докажите, что а) m и АС – скрещивающиеся прямые – и найдите угол между ними; б) m и AD – скрещивающиеся прямые – и найдите угол между ними, если АВС 128 0 . А В D С 128 0 128 0
Слайд 34
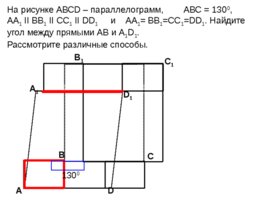
А D С А 1 B 1 С 1 D 1 В 130 0 130 0 На рисунке АВС D – параллелограмм, АВС 130 0 , АА 1 II BB 1 II CC 1 II DD 1 и АА 1 BB 1 CC 1 DD 1 . Найдите угол между прямыми АВ и А 1 D 1 . Рассмотрите различные способы.
Слайд 35
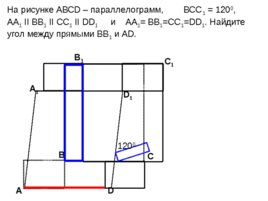
А D С А 1 B 1 С 1 D 1 В 1 2 0 0 На рисунке АВС D – параллелограмм, ВС C 1 1 2 0 0 , АА 1 II BB 1 II CC 1 II DD 1 и АА 1 BB 1 CC 1 DD 1 . Найдите угол между прямыми ВВ 1 и А D .
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.
