Презентация - Скрещивающиеся прямые (решение задач)

Скрещивающиеся Л. С. Атанасян Геометрия 10 класс прямые

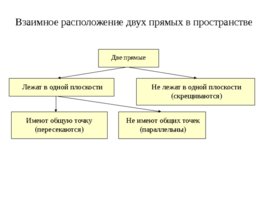
Две прямые Лежат в одной плоскости Не лежат в одной плоскости (скрещиваются) Имеют общую точку (пересекаются) Не имеют общих точек (параллельны) Взаимное расположение двух прямых в пространстве

Ответ: Нет. Всегда ли две не пересекающиеся прямые в пространстве скрещиваются? Упражнение 1

Ответ: A 1 D 1 ; B 1 C 1 ; DD 1 ; CC 1 . Назовите прямые, проходящие через вершины куба A D 1 и скрещивающиеся с прямой AB . Упражнение 2

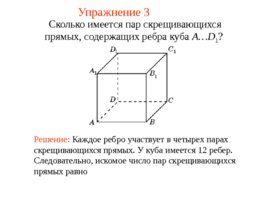
Решение: Каждое ребро участвует в четырех парах скрещивающихся прямых. У куба имеется 12 ребер. Следовательно, искомое число пар скрещивающихся прямых равно Сколько имеется пар скрещивающихся прямых, содержащих ребра куба A D 1 ? Упражнение 3

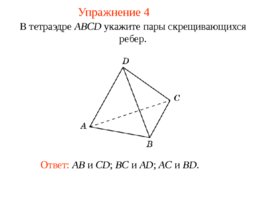
В тетраэдре ABCD укажите пары скрещивающихся ребер. Ответ: AB и CD ; BC и AD ; AC и BD . Упражнение 4

Ответ: Прямая GH пересекает плоскость ABB 1 в точке, не принадлежащей прямой EF . Следовательно, по признаку скрещивающихся прямых, прямые EF и GH скрещиваются. Как в пространстве расположены прямые EF и GH , проведенные в плоскостях граней куба A D 1 ? Упражнение 5

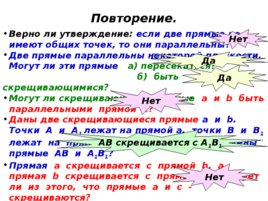
Повторение. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? Две прямые параллельны некоторой плоскости. Могут ли эти прямые а) пересекаться? б) быть скрещивающимися? Могут ли скрещивающиеся прямые а и b быть параллельными прямой с ? Даны две скрещивающиеся прямые а и b . Точки А и А 1 лежат на прямой а , точки В и В 1 лежат на прямой b . Как будут расположены прямые АВ и А 1 В 1 ? Прямая а скрещивается с прямой b , а прямая b скрещивается с прямой с . Следует ли из этого, что прямые а и с - скрещиваются? Нет Да Нет Нет Да АВ скрещивается с А 1 В 1

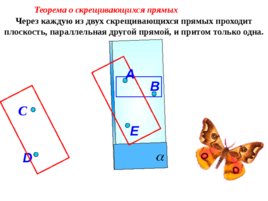
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теорема о скрещивающихся прямых D С B E A

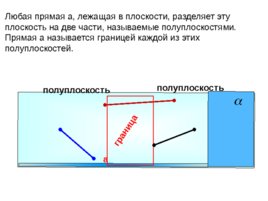
полуплоскость полуплоскость граница Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. а

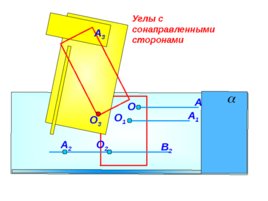
Углы с сонаправленными сторонами A О О 1 О 2 A 1 В 2 A 2 О 3 A 3

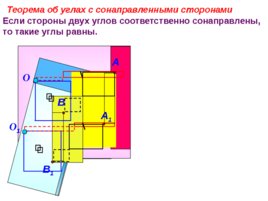
Если стороны двух углов соответственно сонаправлены, то такие углы равны. Теорема об углах с сонаправленными сторонами О О 1 A 1 A B 1 B

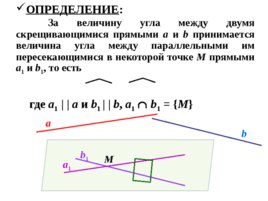
ОПРЕДЕЛЕНИЕ : За величину угла между двумя скрещивающимися прямыми a и b принимается величина угла между параллельными им пересекающимися в некоторой точке M прямыми a 1 и b 1 , то есть где a 1 a и b 1 b , a 1 b 1 M a b M a 1 b 1

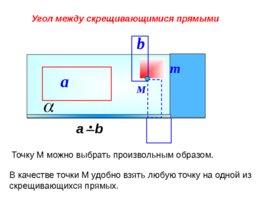
Угол между скрещивающимися прямыми а b a b М Точку М можно выбрать произвольным образом. m В качестве точки М удобно взять любую точку на одной из скрещивающихся прямых.

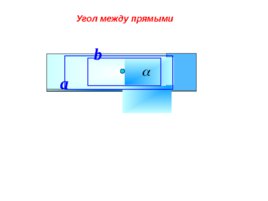
Угол между прямыми a b

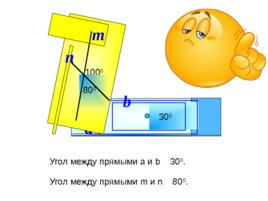
a b 30 0 n 10 0 0 m 8 0 0 Угол между прямыми m и n 80 0 . Угол между прямыми а и b 30 0 .

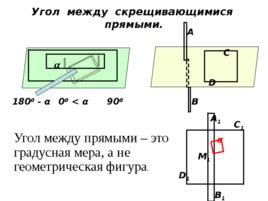
Угол между скрещивающимися прямыми. α 180 0 - α 0 0 α 90 0 А В D С А 1 В 1 С 1 D 1 α М 1 Угол между прямыми – это градусная мера, а не геометрическая фигура .

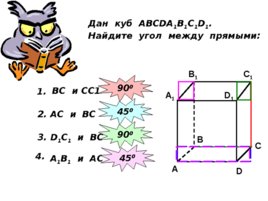
C 1 C A 1 B 1 D 1 A B D Дан куб АВС D А 1 В 1 С 1 D 1 . Найдите угол между прямыми: 1. ВС и СС1 2. 90 0 АС и ВС 45 0 3. D 1 С 1 и ВС 90 0 4 . А 1 В 1 и АС 45 0

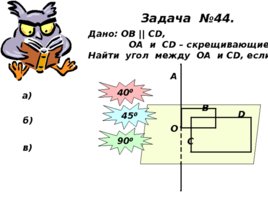
Задача №44. Дано: ОВ С D , ОА и С D – скрещивающиеся. Найти угол между ОА и С D , если: О В C D A а) 40 0 б) 45 0 в) 90 0

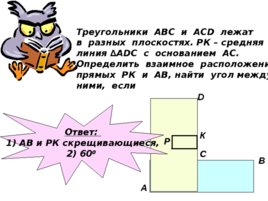
Треугольники АВС и АС D лежат в разных плоскостях. РК – средняя линия А DC с основанием АС. Определить взаимное расположение прямых РК и АВ, найти угол между ними, если А В С D P К Ответ: 1) АВ и РК скрещивающиеся, 2) 60 0

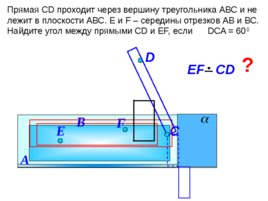
Прямая С D проходит через вершину треугольника АВС и не лежит в плоскости АВС. E и F – середины отрезков АВ и ВС. Найдите угол между прямыми С D и EF , если DCA 60 0 D В EF С D А C ? F E

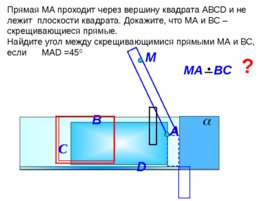
Прямая МА проходит через вершину квадрата АВС D и не лежит плоскости квадрата. Докажите, что МА и ВС – скрещивающиеся прямые. Найдите угол между скрещивающимися прямыми МА и ВС, если МА D 45 0. М D МА ВС С А ? B

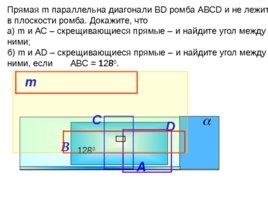
т Прямая m параллельна диагонали В D ромба АВС D и не лежит в плоскости ромба. Докажите, что а) m и АС – скрещивающиеся прямые – и найдите угол между ними; б) m и AD – скрещивающиеся прямые – и найдите угол между ними, если АВС 128 0 . А В D С 128 0 128 0

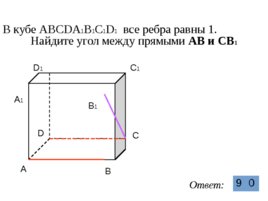
В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми АВ и CB 1 A C B D A A 1 D 1 C 1 B 1 Ответ: 9 0

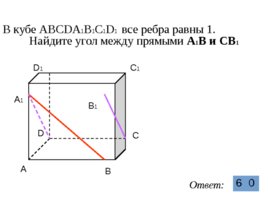
В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми А 1 В и CB 1 A A C B D A 1 D 1 C 1 B 1 Ответ: 6 0

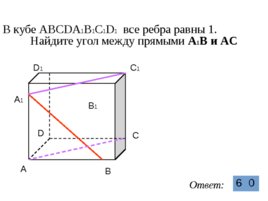
В кубе ABCDA 1 B 1 C 1 D 1 все ребра равны 1. Найдите угол между прямыми А 1 В и AC A A C B D A 1 D 1 C 1 B 1 Ответ: 6 0

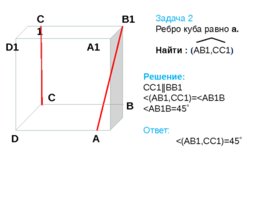
A A1 B B1 C C1 D D1 Задача 2 Ребро куба равно а. Найти : ( АВ1,СС1 ) Решение: СС1 ВВ1 Ответ:

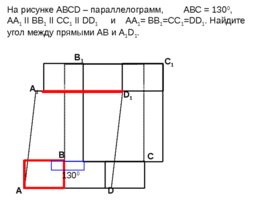
А D С А 1 B 1 С 1 D 1 В 130 0 130 0 На рисунке АВС D – параллелограмм, АВС 130 0 , АА 1 II BB 1 II CC 1 II DD 1 и АА 1 BB 1 CC 1 DD 1 . Найдите угол между прямыми АВ и А 1 D 1 .

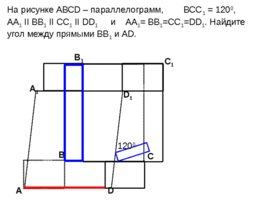
А D С А 1 B 1 С 1 D 1 В 1 2 0 0 На рисунке АВС D – параллелограмм, ВС C 1 1 2 0 0 , АА 1 II BB 1 II CC 1 II DD 1 и АА 1 BB 1 CC 1 DD 1 . Найдите угол между прямыми ВВ 1 и А D .