Презентация - Параллельное проектирование

Параллельное проектирование Гордиенко Алина 10 класс МБОУ СО Ш № 15 пос. Штыково

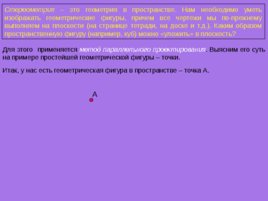
Стереометрия – это геометрия в пространстве. Нам необходимо уметь изображать геометрические фигуры, причем все чертежи мы по-прежнему выполняем на плоскости (на странице тетради, на доске и т.д.). Каким образом пространственную фигуру (например, куб) можно «уложить» в плоскость? Для этого применяется метод параллельного проектирования . Выясним его суть на примере простейшей геометрической фигуры – точки. Итак, у нас есть геометрическая фигура в пространстве – точка А. А

При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции А а

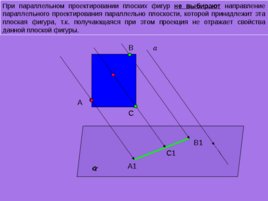
При параллельном проектировании плоских фигур не выбирают направление параллельного проектирования параллельно плоскости, которой принадлежит эта плоская фигура, т.к. получающаяся при этом проекция не отражает свойства данной плоской фигуры. А а B C А1 B 1 C 1

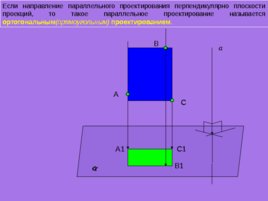
Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным (прямоугольным) проектированием . А а B C А1 B 1 C 1

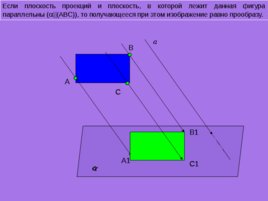
Если плоскость проекций и плоскость, в которой лежит данная фигура параллельны ( (АВС)) , то получающееся при этом изображение равно прообразу. А а B C А1 B 1 C 1

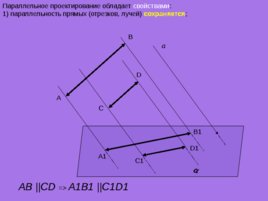
Параллельное проектирование обладает свойствами : 1) параллельность прямых (отрезков, лучей) сохраняется ; а A D C B A 1 D 1 C 1 B 1 AB CD A1B1 C1D1

2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется ; Параллельное проектирование обладает свойствами : параллельность прямых (отрезков, лучей) сохраняется ; а A D C B A1 D1 C1 B1 Если, например, АВ 2 CD , то А 1 В 1 2 C1D1 или М М 1

Параллельное проектирование обладает свойствами : параллельность прямых (отрезков, лучей) сохраняется ; а A B A1 B1 3) Линейные размеры плоских фигур(длины отрезков, величины углов) не сохраняются (исключение ортогональное проектирование). 2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется ; β β 1 C C1

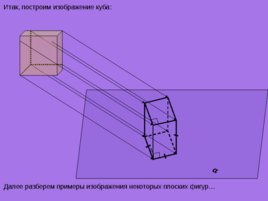
Итак, построим изображение куба: Далее разберем примеры изображения некоторых плоских фигур

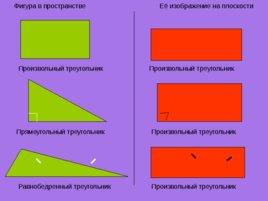
Фигура в пространстве Её изображение на плоскости Произвольный треугольник Произвольный треугольник Прямоугольный треугольник Произвольный треугольник Равнобедренный треугольник Произвольный треугольник

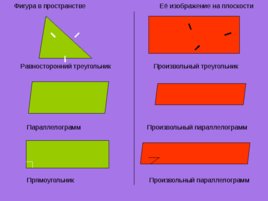
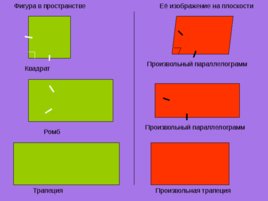
Фигура в пространстве Её изображение на плоскости Равносторонний треугольник Произвольный треугольник Параллелограмм Произвольный параллелограмм Прямоугольник Произвольный параллелограмм

Фигура в пространстве Её изображение на плоскости Квадрат Произвольный параллелограмм Трапеция Произвольная трапеция Произвольный параллелограмм Ромб

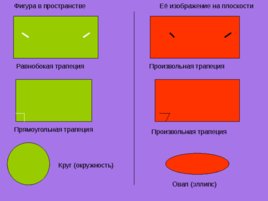
Фигура в пространстве Её изображение на плоскости Равнобокая трапеция Произвольная трапеция Прямоугольная трапеция Произвольная трапеция Круг (окружность) Овал (эллипс)

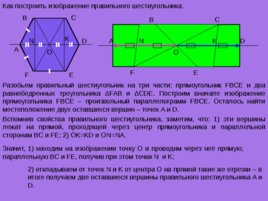
A B C D E F O Как построить изображение правильного шестиугольника. F A B C D E Разобьем правильный шестиугольник на три части: прямоугольник FBCE и два равнобедренных треугольника Δ FAB и Δ CDE . Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE . Осталось найти местоположение двух оставшихся вершин – точек A и D . Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE ; 2) OK KD и ON NA . K N Значит, 1) находим на изображении точку О и проводим через неё прямую, параллельную BC и FE , получив при этом точки N и K ; O N K 2) откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D .