Презентация - Открытый урок. Веселой и полезной. 9 Класс.. Алгебры

Открытый урок
веселой и полезной
9 класс.
алгебры
Бондаренко Н.И.

Девиз урока
«КНИГА – КНИГОЙ, А МОЗГАМИ ДВИГАЙ» (В. В.Маяковский). Задачи урока Повторить и закрепить умения: Строить и читать графики степенной функции; Графически решать уравнения, неравенства, системы.

Найти область определения функции:
а) (- ; 1,5); б)(- ; -4]  (5;+) в)(- ; -2] [0.5;+) г) ( -; +);

Нам знакомы функции
у = х
у = х2
Прямая
Парабола
у = х3
Кубическая парабола
Гипербола

Все эти функции являются частными случаями степенной функции
у = хn, у = х-n где n – заданное натуральное число
Свойства и график степенной функции зависят от значения показателя n

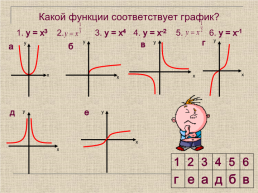
Какой функции соответствует график? 1. у = х3 2. 3. у = х4 4. у = х-2 5. 6. у = х-1
1.2.3.4.5.6
г.е.а.д.б.в

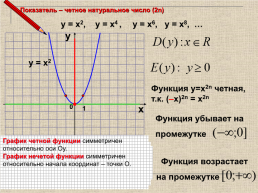
Показатель – четное натуральное число (2n)
у = х2, у = х4 , у = х6, у = х8, …
у
у = х2
Функция у=х2n четная, т.к. (–х)2n = х2n
х
График четной функции симметричен относительно оси Оу. График нечетой функции симметричен относительно начала координат – точки О.
Область значений функции – множество значений, которые может принимать переменная у
Область определения функции – значения, которые может принимать переменная х

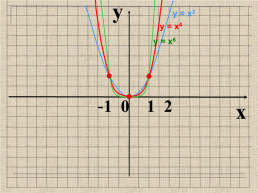
y
у = х2
у = х4
у = х6
-1 0 1 2
x

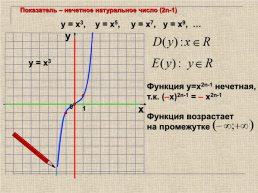
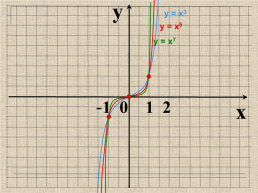
Показатель – нечетное натуральное число (2n-1)
у = х3, у = х5, у = х7, у = х9, …
у
у = х3
Функция у=х2n-1 нечетная, т.к. (–х)2n-1 = – х2n-1
х

y
у = х3
у = х5
у = х7
-1 0 1 2
x

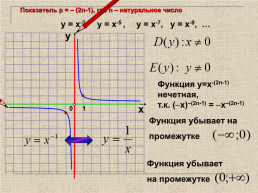
Показатель р = – (2n-1), где n – натуральное число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
Функция у=х-(2n-1) нечетная, т.к. (–х)–(2n-1) = –х–(2n-1)
х

y
у = х-1
у = х-3
у = х-5
-1 0 1 2
x

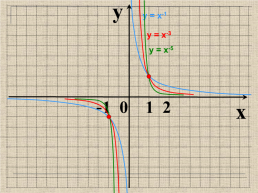
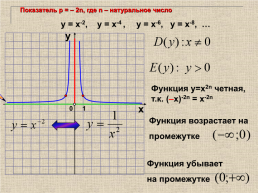
Показатель р = – 2n, где n – натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
Функция у=х2n четная, т.к. (–х)-2n = х-2n
х

Что мы должны уметь:
Уметь строить график степенной функции. Уметь по графику составлять формулы функции. Уметь строить и читать кусочные функции. Уметь графически решать уравнения, неравенства и их системы.

СПАСИБО ЗА УРОК.