Презентация - Решение задач на теорему Пифагора

Решение задач на теорему Пифагора

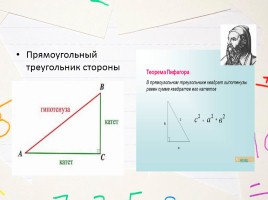
Прямоугольный треугольник стороны

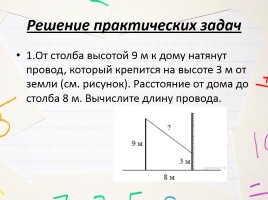
Решение практических задач
1.От стол­ба вы­со­той 9 м к дому на­тя­нут про­вод, ко­то­рый кре­пит­ся на вы­со­те 3 м от земли (см. ри­су­нок). Рас­сто­я­ние от дома до стол­ба 8 м. Вы­чис­ли­те длину про­во­да.

Решение.
Проведём отрезок, параллельный горизонтальной прямой. Таким образом, задача сводится к нахождению гипотенузы прямоугольного треугольника; обозначим её за По теореме Пифагора:     Ответ: 10.

2.Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?

Решение
Задача сводится к нахождению катета прямоугольного треугольника, по теореме Пифагора он равен:   Ответ: 2,4.

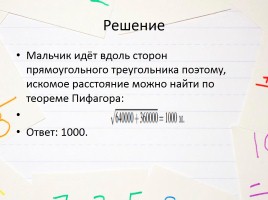
Мальчик прошел от дома по направ­ле­нию на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?

Решение
Мальчик идёт вдоль сторон прямоугольного треугольника поэтому, искомое расстояние можно найти по теореме Пифагора:   Ответ: 1000.

Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии (в метрах) от дома оказалась девочка?

Решение
Девочка идёт вдоль прямоугольной трапеции, в которой длина боковой стороны, не перпендикулярной основаниям, есть искомое расстояние, которое можно найти по теореме Пифагора:   Ответ: 500.

Глубина крепостного рва равна 8 м, ширина 5 м, а высота крепостной стены от ее основания 20 м. Длина лестницы, по которой можно взобраться на стену, на 2 м больше, чем расстояние от края рва до верхней точки стены (см. рис.). Найдите длину лестницы.

Решение
Расстояние AB — гипотенуза прямоугольного треугольника с катетами 5 м и 20 − 8 = 12 м. Тем самым, длина AB равна 13 м, а длина лестницы равна 15 м.   Ответ: 15.

Лестница соединяет точки A и B и состоит из 35 ступеней. Высота каждой ступени равна 14 см, а длина — 48 см. Найдите расстояние между точками A и B (в метрах).

Высота и длина каждой ступени составляют катеты прямоугольного треугольника, найдём гипотенузу этого треугольника по теореме Пифагора:     Всего ступеней 35, следовательно, расстояние между точками A и B равно 50 · 35 = 1750 см = 17,5 м.   Ответ: 17,5.

7.Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.

Решение
Задачу можно свести к нахождению гипотенузы прямоугольного треугольника. По теореме Пифагора её длина равна
Ответ: 17.

8. От столба к дому натянут провод дли­ной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.

Решение
Проведём отрезок, параллельный горизонтальной прямой. Таким образом, задача сводится к нахождению катета прямоугольного треугольника. Обозначим искомую длину за По теореме Пифагора:   тогда   Ответ: 12.  

Длина стремянки в сложенном виде равна 1,85 м, а её высота в разложенном виде составляет 1,48 м. Найдите расстояние (в метрах) между основаниями стремянки в разложенном виде.

Решение
Данная задача сводится к нахождению катета прямоугольного треугольника. Пусть — искомое расстояние, тогда:     Ответ: 2,22.

10. Пожарную лестницу длиной 13 м приставили к окну пятого этажа дома. Нижний конец лестницы отстоит от стены на 5 м. На какой высоте расположено окно? Ответ дайте в метрах.

Решение
Задача сводится к нахождению катета прямоугольного треугольника:     Ответ: 12.  

Домашнее задание
1. Почему теорема долгое время называлась "теоремой невесты"? 2. Какие треугольники называют пифагоровыми?