Презентация - Алгебра логики
Нужно больше вариантов? Смотреть похожие Нажмите для полного просмотра 
|
Распечатать
- Уникальность: 92%
- Слайдов: 16
- Просмотров: 6011
- Скачиваний: 3181
- Размер: 0.09 MB
- Онлайн: Да
- Формат: ppt / pptx
Слайды и текст этой онлайн презентации
Слайд 1

Алгебра логики
Слайд 2

ЛОГИКА
Аристотель заложил основы формальной логики. Он отделил логические формы мышления от его содержания.
Логика – это наука о формах и способах мышления
Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Основными формами мышления являются понятие, высказывание (суждение), умозаключение.
Аристотель заложил основы формальной логики. Он отделил логические формы мышления от его содержания.
Логика – это наука о формах и способах мышления
Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Основными формами мышления являются понятие, высказывание (суждение), умозаключение.
Слайд 3

ПОНЯТИЕ
Понятие – это форма мышления, отражающая наиболее существенные признаки предмета, отличающие его от других предметов.
Содержание понятия составляет совокупность существенных признаков предмета.
Понятие «компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации и обладают монитором и клавиатурой.
Объём понятия определяется совокупностью предметов, на которую понятие распространяется.
Чем больше объём понятия, тем меньше его содержание, и наоборот, чем больше содержание понятия, тем меньше его объём.
Понятие «карманный компьютер» охватывает меньший объём, чем понятие «компьютер», но обладает большей содержательностью.
Понятие – это форма мышления, отражающая наиболее существенные признаки предмета, отличающие его от других предметов.
Содержание понятия составляет совокупность существенных признаков предмета.
Понятие «компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации и обладают монитором и клавиатурой.
Объём понятия определяется совокупностью предметов, на которую понятие распространяется.
Чем больше объём понятия, тем меньше его содержание, и наоборот, чем больше содержание понятия, тем меньше его объём.
Понятие «карманный компьютер» охватывает меньший объём, чем понятие «компьютер», но обладает большей содержательностью.
Слайд 4
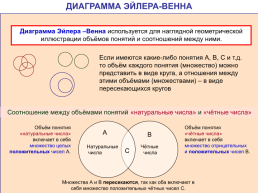
ДИАГРАММА ЭЙЛЕРА-ВЕННА
Диаграмма Эйлера –Венна используется для наглядной геометрической иллюстрации объёмов понятий и соотношений между ними.
Если имеются какие-либо понятия А, В, С и т.д. то объём каждого понятия (множество) можно представить в виде круга, а отношения между этими объёмами (множествами) – в виде пересекающихся кругов
Соотношение между объёмами понятий «натуральные числа» и «чётные числа»
Натуральные числа
Чётные числа
Объём понятия «натуральные числа» включает в себя множество целых положительных чисел А.
Объём понятия «чётные числа» включает в себя множество отрицательных и положительных чисел В.
А
В
С
Множества А и В пересекаются, так как оба включают в себя множество положительных чётных чисел С.
Диаграмма Эйлера –Венна используется для наглядной геометрической иллюстрации объёмов понятий и соотношений между ними.
Если имеются какие-либо понятия А, В, С и т.д. то объём каждого понятия (множество) можно представить в виде круга, а отношения между этими объёмами (множествами) – в виде пересекающихся кругов
Соотношение между объёмами понятий «натуральные числа» и «чётные числа»
Натуральные числа
Чётные числа
Объём понятия «натуральные числа» включает в себя множество целых положительных чисел А.
Объём понятия «чётные числа» включает в себя множество отрицательных и положительных чисел В.
А
В
С
Множества А и В пересекаются, так как оба включают в себя множество положительных чётных чисел С.
Слайд 5

ВЫСКАЗЫВАНИЕ
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними.
Высказывание может быть либо истинно, либо ложно.
В истинном высказывании связь понятий правильно отражает свойства и отношения реальных вещей.
В ложном высказывании связь понятий искажает объективные отношения, не соответствует реальной действительности.
«Два умножить на два равно четырём»
«Два умножить на два равно пяти»
В простом высказывании никакая его часть сама не является высказыванием. «Наступила весна» Составное (сложное) высказывание состоит из простых высказываний. «Наступила весна, и прилетели грачи»
В математической логике рассматриваются предикаты, т.е. функциональные зависимости от неопределенных понятий (терминов), которые можно сравнить с переменными в уравнении.
Порядок предикатов равен числу неопределенных терминов.
В предикатах первого порядка не определен один термин, в предикатах второго порядка – два…
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними.
Высказывание может быть либо истинно, либо ложно.
В истинном высказывании связь понятий правильно отражает свойства и отношения реальных вещей.
В ложном высказывании связь понятий искажает объективные отношения, не соответствует реальной действительности.
«Два умножить на два равно четырём»
«Два умножить на два равно пяти»
В простом высказывании никакая его часть сама не является высказыванием. «Наступила весна» Составное (сложное) высказывание состоит из простых высказываний. «Наступила весна, и прилетели грачи»
В математической логике рассматриваются предикаты, т.е. функциональные зависимости от неопределенных понятий (терминов), которые можно сравнить с переменными в уравнении.
Порядок предикатов равен числу неопределенных терминов.
В предикатах первого порядка не определен один термин, в предикатах второго порядка – два…
Слайд 6

УМОЗАКЛЮЧЕНИЕ
Умозаключение – это форма мышления, с помощью которой из одного или нескольких высказываний (посылок) может быть получено новое высказывание (вывод).
Умозаключения бывают дедуктивные, индуктивные и по аналогии.
«Все металлы электропроводны» «Ртуть является металлом» ___________________________________________________ «Ртуть электропроводна»
В дедуктивных умозаключениях рассуждения ведутся от общего к частному
«Металлы железо и цинк электропроводны» ___________________________________________________________________ «Все металлы электропроводны»
В индуктивных умозаключениях рассуждения ведутся от частного к общему
В умозаключениях по аналогии движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов к общности других свойств и отношений
«Химический состав Солнца и Земли сходен» «На Солнце есть химический элемент гелий» ___________________________________________________________________ «На Земле тоже должен быть химический элемент гелий»
Умозаключение – это форма мышления, с помощью которой из одного или нескольких высказываний (посылок) может быть получено новое высказывание (вывод).
Умозаключения бывают дедуктивные, индуктивные и по аналогии.
«Все металлы электропроводны» «Ртуть является металлом» ___________________________________________________ «Ртуть электропроводна»
В дедуктивных умозаключениях рассуждения ведутся от общего к частному
«Металлы железо и цинк электропроводны» ___________________________________________________________________ «Все металлы электропроводны»
В индуктивных умозаключениях рассуждения ведутся от частного к общему
В умозаключениях по аналогии движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов к общности других свойств и отношений
«Химический состав Солнца и Земли сходен» «На Солнце есть химический элемент гелий» ___________________________________________________________________ «На Земле тоже должен быть химический элемент гелий»
Слайд 7

ДОКАЗАТЕЛЬСТВО
Доказательство есть мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других несомненных, ранее обоснованных доводов.
Доказательство по своей логической форме не отличается от умозаключения. Однако, в умозаключении заранее исходят из истинности посылок, а в доказательстве подвергается логической проверке истинность самих посылок.
Пример умозаключений – геометрические доказательства
«Все углы треугольника равны» ___________________________________________________________________ «Этот треугольник равносторонний»
Доказательство есть мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других несомненных, ранее обоснованных доводов.
Доказательство по своей логической форме не отличается от умозаключения. Однако, в умозаключении заранее исходят из истинности посылок, а в доказательстве подвергается логической проверке истинность самих посылок.
Пример умозаключений – геометрические доказательства
«Все углы треугольника равны» ___________________________________________________________________ «Этот треугольник равносторонний»
Слайд 8

Составное высказывание на естественном языке образуется с помощью связок и, или, не,
которые в алгебре логики заменяются на логические операции умножения, сложения и отрицания.
Логические операции задаются таблицами истинности.
Слайд 9

Логическое умножение (конъюнкция)
Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией.
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией.
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Слайд 10
Логическое умножение (конъюнкция)
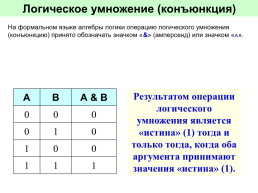
На формальном языке алгебры логики операцию логического умножения (конъюнкцию) принято обозначать значком «&» (амперсенд) или значком «».
А.В.А & В
0.0.0
0.1.0
1.0.0
1.1.1
Результатом операции логического умножения является «истина» (1) тогда и только тогда, когда оба аргумента принимают значения «истина» (1).
На формальном языке алгебры логики операцию логического умножения (конъюнкцию) принято обозначать значком «&» (амперсенд) или значком «».
А.В.А & В
0.0.0
0.1.0
1.0.0
1.1.1
Результатом операции логического умножения является «истина» (1) тогда и только тогда, когда оба аргумента принимают значения «истина» (1).
Слайд 11

Логическое сложение (дизъюнкция)
Объединение двух (или нескольких) высказываний в одно с помощью союза «или» называется операцией логического сложения или дизъюнкцией.
Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Объединение двух (или нескольких) высказываний в одно с помощью союза «или» называется операцией логического сложения или дизъюнкцией.
Составное высказывание, образованное в результате операции логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Слайд 12
Логическое сложение (дизъюнкция)
На формальном языке алгебры логики операцию логического операцию логического сложения (дизъюнкцию) принято обозначать значком «».
Значение логической операции сложения задается с помощью таблицы истинности.
Результатом операции логического сложения является «ложь» (0) тогда и только тогда, когда оба аргумента принимают значения «ложь» (0).
А.В.А v В
0.0.0
0.1.1
1.0.1
1.1.1
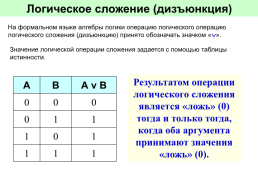
На формальном языке алгебры логики операцию логического операцию логического сложения (дизъюнкцию) принято обозначать значком «».
Значение логической операции сложения задается с помощью таблицы истинности.
Результатом операции логического сложения является «ложь» (0) тогда и только тогда, когда оба аргумента принимают значения «ложь» (0).
А.В.А v В
0.0.0
0.1.1
1.0.1
1.1.1
Слайд 13

Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.
Логическое отрицание (инверсия) получает из истинного высказывания ложное и, наоборот, из ложного — истинное.
Высказывание «Два умножить на два равно четырем» истинно. Высказывание, образованное с помощью операции логического отрицания, «Два умножить на два не равно четырем» ложно.
Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией.
Логическое отрицание (инверсия) получает из истинного высказывания ложное и, наоборот, из ложного — истинное.
Высказывание «Два умножить на два равно четырем» истинно. Высказывание, образованное с помощью операции логического отрицания, «Два умножить на два не равно четырем» ложно.
Слайд 14
Логическое отрицание (инверсия)
На формальном языке алгебры логики операцию логического отрицания (инверсию) над логическим высказыванием А принято обозначать или А, или А.
Значение логической операции отрицания задается с помощью таблицы истинности.
Результатом операции логического отрицания является «истина» (1), когда аргумент принимает значение «ложь» (0), и значение «ложь» (0), когда аргумент принимает значение «истина» (1).
А.А
0.1
1.0
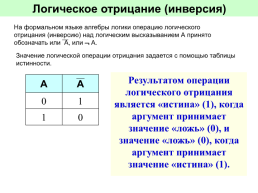
На формальном языке алгебры логики операцию логического отрицания (инверсию) над логическим высказыванием А принято обозначать или А, или А.
Значение логической операции отрицания задается с помощью таблицы истинности.
Результатом операции логического отрицания является «истина» (1), когда аргумент принимает значение «ложь» (0), и значение «ложь» (0), когда аргумент принимает значение «истина» (1).
А.А
0.1
1.0
Слайд 15

Импликация - логическое следование
Результат логического следования является ложным тогда и только тогда, когда из истины следует ложь.
От лат. implicatio – тесно связывать
В переводе на естественный язык «если А, то В» «В, если А» «Когда А, тогда В» «А достаточно для В» «А только тогда, когда В»
Таблица истинности функции логического следования
A.B.F=A B
0.0.1
0.1.1
1.0.0
1.1.1
Пример: Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 - простое» = ЛОЖЬ А В – «Если число 10 – четное, то оно - отрицательное» - ЛОЖЬ А С – «Число 10 простое, если четное» - ЛОЖЬ «Если число делится на 10, то оно делится на 5» ИСТИНА
А – условие, В - следствие
Результат логического следования является ложным тогда и только тогда, когда из истины следует ложь.
От лат. implicatio – тесно связывать
В переводе на естественный язык «если А, то В» «В, если А» «Когда А, тогда В» «А достаточно для В» «А только тогда, когда В»
Таблица истинности функции логического следования
A.B.F=A B
0.0.1
0.1.1
1.0.0
1.1.1
Пример: Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 - простое» = ЛОЖЬ А В – «Если число 10 – четное, то оно - отрицательное» - ЛОЖЬ А С – «Число 10 простое, если четное» - ЛОЖЬ «Если число делится на 10, то оно делится на 5» ИСТИНА
А – условие, В - следствие
Слайд 16

Эквивалентность - логическое равенство
Результат логического равенства является истинным тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
От лат. aeguivalens – равноценное
В переводе на естественный язык «А эквивалентно В» «А только тогда и только тогда, когда В»
Таблица истинности функции логического равенства
A.B.F=A B
0.0.1
0.1.0
1.0.0
1.1.1
Пример: Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 - простое» = ЛОЖЬ А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА
=,
Результат логического равенства является истинным тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
От лат. aeguivalens – равноценное
В переводе на естественный язык «А эквивалентно В» «А только тогда и только тогда, когда В»
Таблица истинности функции логического равенства
A.B.F=A B
0.0.1
0.1.0
1.0.0
1.1.1
Пример: Даны высказывания А – «Число 10 – четное» = ИСТИНА В – «Число 10 – отрицательное» = ЛОЖЬ С – «Число 10 - простое» = ЛОЖЬ А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА
=,
^ Наверх
X
Благодарим за оценку!
Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.







