Слайды и текст этой онлайн презентации
Слайд 1
Решение задач на применение производной
(задачи В8 и В11)
Слайд 2
Если функция дифференцируема на всей области определения , то графиком функции является
гладкая кривая
Слайд 3
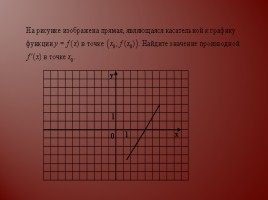
Касательная
(х๐;f(x๐)) – координаты точки касания
Уравнение касательной
y=f´(x๐)·(x-x๐)+f(x๐)
y=kx+b
Слайд 4
Геометрический смысл производной
k=f´(x๐)=tgα
k- угловой коэффициент касательной
α-угол наклона касательной к положительному направлению оси Ох
k>0, α-острый
k<0, α-тупой
k=0, касательная параллельна оси Ох (α=0)
Слайд 5
Физический смысл производной
Y=S(t)- зависимость пути от времени
S´(t)=V(t)- зависимость скорости от времени
S´´(t)=V´(t)=a(t)-зависимость ускорения от времени
Слайд 6
Нахождение промежутков монотонности
f´(x)=0- условие нахождения критических точек
Если f´(x)>0 на промежутке (a;b), то функция возрастает на промежутке (a;b)
Если f´(x)<0 на промежутке (a;b), то функция убывает на промежутке (a;b)
Слайд 7
Нахождение точек экстремума и экстремумов функции
1.Область определения функции
2.Найти производную
3.Найти критические точки
f ’ (x) + - +
4. f(x) x₁ x₂ x
5.Ответ
Слайд 8
Нахождение наибольшего или наименьшего значений функции на отрезке
1.найти область определения функции
2.найти производную функции
3.найти критические точки
4.Найти значения функции на концах отрезка и в критических точках, принадлежащих данному отрезку
5.Выбрать наибольшее или наименьшее значения функции
Слайд 10
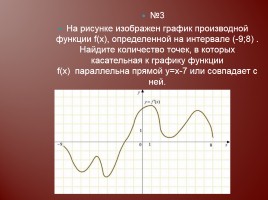
№3
На рисунке изображен график производной функции f(x), определенной на интервале (-9;8) . Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=x-7 или совпадает с ней.
Слайд 11
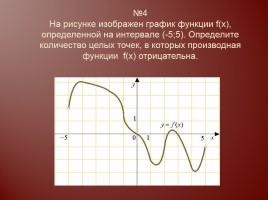
№4 На рисунке изображен график функции f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции f(x) отрицательна.
Слайд 12
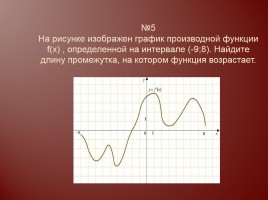
№5 На рисунке изображен график производной функции f(x) , определенной на интервале (-9;8). Найдите длину промежутка, на котором функция возрастает.
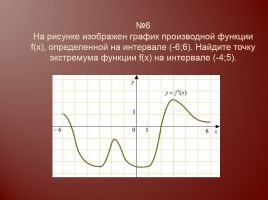
Слайд 13
№6 На рисунке изображен график производной функции f(x), определенной на интервале (-6;6). Найдите точку экстремума функции f(x) на интервале (-4;5).
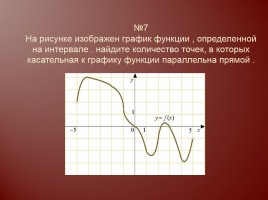
Слайд 14
№7 На рисунке изображен график функции , определенной на интервале . найдите количество точек, в которых касательная к графику функции параллельна прямой .
 Пропорциональные величины (приведены примеры решения задач на их применение)
Пропорциональные величины (приведены примеры решения задач на их применение) Дробно-рациональные уравнения. Применение при решении задач
Дробно-рациональные уравнения. Применение при решении задач Теорема о трех перпендикулярах, ее применение при решении задач
Теорема о трех перпендикулярах, ее применение при решении задач Теорема Виета и её применение для решения задач
Теорема Виета и её применение для решения задач Применение признаков подобия треугольников к решению практических задач
Применение признаков подобия треугольников к решению практических задач Использование таблиц для решения задач
Использование таблиц для решения задач Урок в 5 классе «Решение практических задач»
Урок в 5 классе «Решение практических задач»